Calculer, lire et interpréter un taux de variation cumulé
le taux de variation cumulé mesure l’évolution d’une donnée sur plusieurs périodes. Il se calcule à partir des taux de variation de chacune des périodes.
Il n’est pas possible d’additionner les taux de variation. Il faut donc transformer chaque taux de variation (TV) en coefficient multiplicateur !
[h5p id="153"]
Il suffit alors, de multiplier ces coefficients multiplicateurs pour connaître le coefficient multiplicateur de l’ensemble de la période.
Ce coefficient multiplicateur peut alors être transformé en taux de variation.
Lecture du résultat : le taux de variation cumulé se lit comme un taux de variation simple. Il faut indiquer s’il y a augmentation ou diminution et le résultat se lit en pourcentage.
Application : Evolution en % du PIB et des Importations de la France
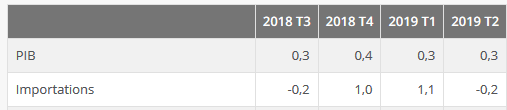
- Transformez le taux de variation du PIB (T3 2018), en coefficient multiplicateur
[su_spoiler title= »Réponse » style= »fancy » icon= »arrow-circle-1″]1.003
.
ici CM = (0.3/100) + 1
[/su_spoiler]
2. Calculez le coefficient multiplicateur qui permet de traduire la croissance du PIB de la France pour la période (du troisième trimestre de 2018 au deuxième trimestre 2019).
[su_spoiler title= »Réponse » style= »fancy » icon= »arrow-circle-1″]Le PIB a été multiplié par 1,013.
Pour répondre à cette question, il n’est pas possible d’additionner les différents taux de variation. Il convient donc de transformer chaque taux de variation en coefficient multiplicateur.
1.003*1.004*1.003*1.003 = 1.013
[/su_spoiler]
3. Exprimez votre résultat en % de variation
[su_spoiler title= »Réponse » style= »fancy » icon= »arrow-circle-1″]Le PIB a augmenté de 1.3 % sur l’ensemble de la période (du troisième trimestre de 2018 au deuxième trimestre 2019) .
Transformation du coefficient multiplicateur en taux de variation : (1.013 – 1) * 100 = 1.3 %
[/su_spoiler]
4. Mesurez ( en %), l’évolution des importations durant la période (du troisième trimestre de 2018 au deuxième trimestre 2019)
[su_spoiler title= »Réponse » style= »fancy » icon= »arrow-circle-1″]Les importations ont augmenté de 1.7 %.
Rappel : Pour répondre à cette question, il n’est pas possible d’additionner les différents taux de variation. Il convient donc de transformer chaque taux de variation en coefficient multiplicateur.
0.998*1.01*1.011*0.998 = 1.017
Soit une augmentation de (1.017-1) * 100 = 1.7 %
[/su_spoiler]
Le Taux de croissance annuel moyen
- Une vidéo pour comprendre
[h5p id= »53″]
source : profdeses.org
Questions :
- Quelle est l’utilité du TCAM ?
- Notez la formule de calcul du TCAM
- Notez la phrase type a utiliser.
- Interpréter un taux de croissance annuel moyen
[iframe width= »560″ height= »315″ src= »https://www.youtube.com/embed/kKUzLdfQQFg » frameborder= »0″ allowfullscreen][/iframe]
Durant les épreuves du baccalauréat, vous n’aurez sans doute pas à calculer un taux de croissance annuel moyen.
Par contre, il est absolument nécessaire que vous sachiez lire un TCAM et que vous soyez capable de faire une phrase pour le décrire. La phrase la plus simple est du type suivant :Entre 1950 et 1975, le PIB a augmenté en moyenne chaque année de 5,3%.
Conseil : éviter les phrases du type : « le TCAM est de 5,3% », qui sont une pure paraphrase du document, et qui ne permettent pas de montrer que vous avez compris la notion de TCAM.
Exercice 1
| Année |
1999
|
2000
|
2001
|
2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
2013
|
| Produit Intérieur Brut (PIB) |
1 705,6
|
1 771,7
|
1 806,3
|
1 826,5
|
1 841,5
|
1 892,8
|
1 923,2
|
1 968,9
|
2 015,4
|
2 019,4
|
1 960,0
|
1 998,5
|
2 040,0
|
2 046,9
|
2 052,7
|
Question 1 : De combien de % a augmenté le PIB entre 1999 et 2009 ?
[su_spoiler title= »Réponse » style= »fancy » icon= »arrow-circle-1″]Le PIB a augmenté de 14,9%. En effet, le pourcentage de variation = (Va-Vd)/Vd = (1960−1705,6)/1705,6 = 14,9%.[/su_spoiler]
Question 2 : Calculer maintenant la croissance qu’il y a eu, en moyenne, chaque année durant cette période.
Question 3 : Rédigez une phrase qui donne le sens de ce résultat.
Exercice 2
Taux de croissance annuels moyens du commerce international et de la production mondiale, mesurée par le PIB mondial (en %)
|
Périodes |
Commerce international |
Production mondiale |
| 1950-1960 | 6.3 |
4.2 |
| 1960-1970 | 8.3 |
5.3 |
| 1970-1980 | 5.2 |
3.6 |
| 1980-1990 | 3.7 |
2.8 |
| 1990-1996 | 5.9 |
1.4 |
| 1996-2000 | 8.2 |
3.4 |
| 2000-2005 | 4.5 |
2.0 |
Source : GATT, OMC, 2013
1) Que signifie les données en gras?
[su_spoiler title= »Réponse » style= »fancy » icon= »arrow-circle-1″]Selon l’Organisation Mondiale du Commerce, chaque année en moyenne entre 1950 et 1960 le commerce international a augmenté de 6,3%
Selon l’Organisation Mondiale du Commerce, chaque année en moyenne entre 1950 et 1960 la production mondiale a augmenté de 4,2%.[/su_spoiler]
2) Sachant que le TCAM du commerce mondial est de 6.3 % entre 1950 et 1960, de combien a augmenté le commerce mondial durant cette période (autrement dit, calculez le taux de croissance global durant cette période )? Et La production mondiale ?
[su_spoiler title= »Réponse » style= »fancy » icon= »arrow-circle-1″] Rappel : Il n’est pas possible d’additionner (ni de multiplier) des taux de variation. Il faut transformer chaque taux de variation en coefficients multiplicateurs !
Pendant 10 ans en moyenne le commerce mondial a augmenté de 6,3% autrement dit il a été multiplié par 1,063 x 1,063 …. x 1,063 pendant 10 fois d’où 1,063 10 ≈ 1,84
Le commerce mondial au augmenté de 84% de 1950 à 1960
Pendant 10 ans en moyenne la production mondiale a augmenté de 4,2% autrement dit il a été multiplié par 1,042 x 1,042 …. x 1,042 pendant 10 fois d’où 1,042 10 ≈ 1,51
La production mondiale a augmenté de 51% de 1950 à 1960.[/su_spoiler]
3) Quelle est l’idée principale du document?
[su_spoiler title= »Réponse » style= »fancy » icon= »arrow-circle-1″]le rythme de croissance du commerce international est toujours plus élevé que celui de la production mondiale. .[/su_spoiler]
Interpréter un taux de croissance annuel
[h5p id="152"]
